Garis Singgung Lingkaran

Pengertian Garis Singgung Lingkaran
  Garis singgung lingkaran adalah garis yang apabila diperpanjang akan memotong lingkaran hanya pada satu titik. Titik potong garis singgung lingkaran dengan lingkaran disebut titik singgung.
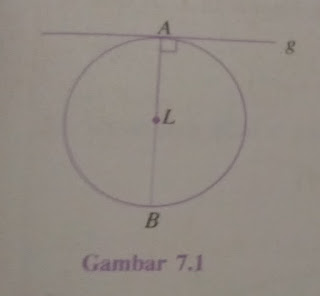
   Garis singgung lingkaran selalu tegak lurus dengan jari-jari atau diameter yang melalui titik singgung. perhatikan gambar dibawah ini:

garis g adalah garis singgung lingkaran L dengan titik singgung A. Garis g tegak  lurus dengan AL (jari-jari lingkaran). Garis g juga tegak lurus dengan AB (diameter lingkaran).

Sifat-sifat Garis Singgung Lingkaran

1.  Garis singgung lingkaran memotong lingkaran hanya pada satu titik.
2. Garis singgung lingkaran tegak lurus dengan jari-jari lingkaran pada titik singgung.
3. Garis yang tegak lurus dengan garis singgung pada titik singgung pasti melalui titik pusat lingkaran.
4. Garis yang tegak lurus dengan diameter dan melalui titik ujungnya adalah garis singgung.

Teorema 1
         Sudut lancip antara garis singgung lingkaran dengan tali busur yang melalui titik singgung. sama dengan sudut keliling yang menghadap tali busur tersebut.

Perhatikan gambar 7.2. Garis FB menyinggung lingkaran L pada titik A, dan AD adalah diameter lingkaran L, maka

       
                             

1. Melukis Garis Singgung Lingkaran Melalui Titik Singgung
       Misal A adalah titik singgung yang terletak pada lingkaran L.
       Langkah-langkah melukis garis singgung pada titik A.
       (i)   Lukislah jari-jari lingkaran L melalui A.
       (ii)  Lukislah garis BAC yang tegak lurus garis LA, dan berpotongan dititik A.
       (iii) Garis BCA merupakan garis singgunglingkaran L (lihat gambar 7.6)

2. Melukis Garis Singgung Lingkaran Melalui Titik Di luar Lingkaran
       Misal P adalah titik yang terletak diluar lingkaran L.

       Langkah-langkah melukis garis singgung yang melalui titik P.
        (i)   Hubungkan titik P dan L
        (ii)  Carilah titik tengah PL (misal Q)
        (iii)  Buatlah lingkaran Q berjari-jari QP atau QL memotong lingkaran L di S dan T.
        (iv)  Hubungkan titik S dan T dengan titik P
        (v)   Garis PS dan PT adalah garis singgung lingkaran L  (Lihat gambar 7.7)


Sekian yang dapat saya sampaikan dalam artikel kali ini,
semoga bermanfaat dan bisa membantu para  pembaca
dalam menyelesaikan permasalahan atau soal tentang materi yang
saya lampirkan
Terimakasih.

RELASI DAN FUNGSI

Pengertian Relasi

Dalama kehidupan sehari-hari, banyak kita temukan hubungan, misalnya hubungan pertemuan, hubungan pekerjaan, dan hubungan kekeluargaan.
    Kata hubungan dapat digunakan untuk menghubungkan dua kelompok (himpunan) dan hubungan tersebut memiliki sebuah "nama". Misalnya ada dua kelompok, yaitu kelompok nama oranng dan nama pekerjaan, lalu kedua kelompok tersebut kita hubungkan dengan nama hubungan "bekerja sebagai", seperti terlihat pada gambar dibawah ini;

Berdasarkan gambar diatas, kita dapat menyatakan hubungan berikut ini:
Yuni bekerja sebagai guru dan pedagang.
Nanda bekerja sebagai pramugari.
Ita bekerja sebagai dokter.
Helen bekerja sebagai dosen.
Hidia tidak mempunyai pekerjaan. digambarkan pada gambar berikut ini.
Jadi, suatu relasi dari kelompok A ke kelompok B adalah memasangkan anggota-anggota kelompok A dengan anggota kelompok B. Relasi dari A ke B dituliskan dengan R : A ---> B
Contoh:
Misalkan ada dua himpunan A dan B dengan
     A = {1,4,9,14}
     B = {1,2,3,4,5}
Relasi dari A ke B diberi nama kuadrat dari.
Relasi tersebut ini:

Pada relasi tersebut dapat kita nyatakan Hal-hal berikut:
       1 adalah kuadrat dari 1
       4 adalah kuadrat dari 2
       9 adalah kuadrat dari 3
       16  adalah kuadrat dari 4
        5 tidak mempunyai pasangan
Definisi Fungsi

    pernyataan sebuah fungsi diberikan berdasarkan kata-kata dalam kehidupan sehari-hari. Berikut ini diberikan pendefinisian fungsi secara matematis.
     Anggap masing-masing unsur himpunan A dapat dipasangkan dengan tepat satu unsur di himpunan B. Pernyataan ini disebut sebuah fungsi. Jika perntyataan itu dinyatakan dengan f maka fungsi ditulis f : A---> B dan dibaca '' f adalah fungsi dari A ke B''.
     Suatu fungsi dari himpunan A ke himpunan B adalah hubungan dari A ke B dimana untuk setiap x elemen A dipasangkan dengan tepat satu y elemen B. jika x elemen A, y elemen B, serta x dipasangkan dengan y, maka y dinamakan bayangan atau peta dari x, atau dapat juga dikatakan x dipetakan ke y dan dituliskan sebagai x ---> y. Himpunan y elemen B yang merupakan peta dari x elemen A disebut range atau daerah hasil fungsi. Himpunan x elemen A disebut domain dan semua anggota himpunan B disebut kodomain.

Notasi suatu Fungsi

• Misalkan fungsi A ke B kita sebut f maka notasi yang digunakan untuk menyatakan fungsi itu adalah:
  
• jika x elemen A, y elemen B, dan y adalah peta (bayangan) dari x maka notasi funsi di atas ditulis sebagai berikut:
  

Penulisan diatas dibaca ''fungsi f memetakan x ke y''
Bila notasi fungsi diatas kita tuliskan dalam bentuk rumus fungsi ( formula fungsi) maka di peroleh:

Conth:
Tuliskan dalam bentuk notasi fungsi:
a. Nyatakan m = 6p^2 - p + 5 sebagai sebuah funsi dalam p.
b. Nyatakan luas L dari sebuah segitiga yang tingginya 10 meter sebagai sebuah fungsi dari alas a.
c. Nyatakan keliling K dari sebuah persegi panjang dengan lebar 8 cm sebagai sebuah fungsi dari panjang p.

Jawab:
a.   Karena m adalah sebuah fungsi dari p, maka notasi fungsinya adalah : f(p) = 6p^2 - p + 5. untuk menyatakan m sebagai variabel bergantung , kita dapat juga menuliskannya sebagai m(p) = 6p^2 - p + 5.
b.   Luas segitiga yang tingginya 10 meter ditentukan oleh formula :
      L = 10a/2 atau L = 5a atau dapat juga ditulliskan dalam notasi fungsi:
        f(a) = 5a atau L(a) = 5a
c    Keliling persegi panjang dengan lebarr 8 cmditentukan oleh:
      K = 2(p + 8) = 2p +16
      Notasi fungsinya ditulis sebagai f(p) = 2p + 16 atau K(p) = 2p + 16






Sekian yang dapatsaya sampailkan dalam artikel kali ini,
semoga bermanfaat dan bisa membantu para pembaca
dalam memecahkan persoalan tentang relasi dan fungsi
Terimakasih.

Penerapan Bentuk Aljabar Dalam Kehidupan Sehari-hari

      Laba (Untung) dan Rugi
       1)  Harga jual, harga beli, laba, dan rugi
             Dalam berdagang, seseorang akan mmbeli suau barang dengan harga tertentu, yang disebut
        harga beli, , kemudian dijualnya dengan harga tertentu yang disebut harga jual.
Bila seorang pedagang menjual barang dengan harga lebih tinggi dari harga beli maka dikatakan ia mendapatkan laba (untung). Sebaliknya, bila menjualnya dengan harga lebih rendah dari harga beli maka dikatakan rugi. Begitupun pula, bila harga jualnya sama dengan harga belinya maka dikatakan impas.
Dari uraian diatas, dapat disimpulkan sebagi berikut:

• Laba (Untung) diperoleh apabila harga jual lebih rendah dari harga beli. sehingga diperoleh rumus:

                       Rugi = harga jual - harga beli

• Rugi diperoleh apabila harga jual lebih rendah dari harga beli. sehingga diperoleh rumus:

                      Rugi = harga beli - harga jual

•  Impas terjadi apabila harga jual sama dengan harga beli

            Jika laba dinyatakan dengan U, rugi dengan R, harga jual dengan J, dan harga beli dengan B
           maka persamaan laba dan rugin dia atas diperoleh:
       
                 U = J - B                                                        R = B - J
                  J = B + U                     dan                            J = B - R
                  B = J - U                                                        B = J + R 
Contoh 1:

Ayu membuet baju untuk di jual. Biaya pembuatan per potong Rp 70.000,00 karena jahitannya ada yang rusak, Ayu menjualnya dengan harga Rp 50.000,00 per potong. Apakah Ayu memperoleh untung rugi? Berapa untung atau ruginya?           Penyelesaian:
           harga beli baju per potong = Rp 70.000,00
           harga jual baju per potong = Rp 50.000,00
           Karena harga jual lebih rendah dari harga beli, berarti Ayu mengalami kerugian sehingga
           kerugian yang dialami Ayu adalah:
           Rugi = harga beli - harga jual
                    = Rp 70.000,00 - Rp 50.000,00
                    = Rp 20.000,00
              Jadi, ayu mengalami kerugian sebesar Rp 20.000,00 
contoh 2:

      Iis membeli gula Rp 5.500,00 per kg, kemudian dijual dan mendapatkan untung Rp 500,00 per kg. Berapa harga jual per kg?

Penyelesaian:
   Harga beli gula per kg =Rp 5.500,00
   Untung gula per kg = Rp 500,00
   Sehingga diperoleh:
   Harga jual = harga beli + untung
                    = Rp 5.500,00 + Rp 500,00
                    = Rp 6.000,00





      2).  Menentuka presentase untung atau rugi dari harga beli

             Kadang-kadang orang menyatakan untung dan rugi dalam bentuk persen, misalnya mendapat untung 20% atau rugi 6%. Untuk menyatakan presentase untung atau rugi, biasanya dari harga beli, tetapi ada juga yang dinyatakan dari harga jual. Namun, demikian bila tidak ada keterangan dari harga beli atau harga jualnya, berarti presentase untung atau ruginya dihitung dari harga beli.

Agar lebih jelasnya, mari kita perhatikan contoh berikut!
Contoh:
1.  Pak surya membeli sepeda motor seharga Rp 10.000.000,00 dan dijual seharga Rp 12.000.000,00. Nyatakan untung atau rugi sebagai persen dari:
a. harga beli                                       b. harga jual
Penyelesaian:
Karena harga jual lebih tinggi dari harga beli, maka untung.
besarnya untung = harga jual - harga beli
                           = Rp 12.000.000,00 - Rp 10.000.000,00
                           = Rp 2.000.000,00
Maka:
a. Untung yang di peroleh bila dinyatakan sebagai presentase dari harga beli adalah:

    
b. Untung yang diperoleh jika dinyatakan sebagai presentase dari harga jual adalah:

 2. Ibu Lina membeli beras seharga Rp 4000,00 per kg, dan dijual seharga Rp 5.000,00 per kg. Berapa persen untung atau rugi yang diperoleh ibu Lina?
  Penyelesaian:
   karena harga jual lebih tinggi dari harga beli, berarti diperoleh untung (laba)
   Besarnya untung = harga jual - harga beli
                               = Rp 5.000,00 - Rp 4.000,00
                               = Rp 1.000,00
Jadi untung yang diperoleh jika dinyatakan sebagai presentase adalah
 

            



sekian yang dapat saya sampaikan dalam artikel kali ini,
semoga bermanfaat dan bisa membantu para pembaca
dalam menyelesaikan permasalah mengenai materi yang telah saya tulis
Terimakasih.