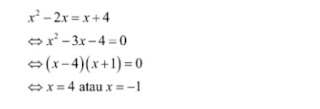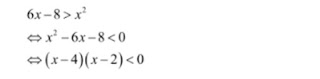Senin, 01 Juni 2020
PERTIDAKSAMAAN
Salah satu penyebab banyaknya pengangguran adalah jumlah
lapangan kerja yang tersedia kurang dari banyaknya angkatan
kerja. agar pengangguran berkurang atau bisa dihilangkan, maka
pemerintah dan pihak pemegang modal harus menciptakan
lapangan kerja lebih dari atau sama dengan banyaknya angakatan
kerja. Hal ini tersebut merupakan salah satu masalah nyata yang
berhubungan dengan konsep pertidaksamaan yang akan dipelajari pada bab ini.
1. Pengertian Pertidaksamaan
Definisi:
Pertidaksamaan adalah kalimat terbuka yang dihubungkan oleh notasi ketidaksamaan
(<, atau >).
2. Interval
Definisi:
Interval adalah himpunan bagian dari himpunan bilangan real.
Interval dapat dituliskan dengan 2 cara, yaitu:
3. Sifat-sifat Pertidaksamaan
Untuk menentukan penyelesaian suatu pertidaksamaan perlu diperhatikan sifat-sifat pertidaksamaan berikut.
Definisi:
a. Untuk a, b dan c bilangan real berikut:
jika a > b dan b > c, maka a > c
jika a < b dan b < c, maka a < c
b. Tanda atau notasi ketidaksamaan tidak berubah jika kedua
ruas pertidaksamaan dijumlahkan atau dikurangi dengan
bilangan yang sama atau dapat dituliskan sebagai berikut:
jika a > b, maka a + c > b + c
jika a < b, maka a + c < b + c
jika a > b, maka a - c > b - c
jika a < b, maka a - c < b - c
c. Tanda atau notasi ketidaksamaan tidak berubah jika kedua
ruas persamaan dikalikan atau dibagi dengan bilangan
positif yang sama atau dapat dituliskan sebagai berikut:
jika a > b dan c > 0, maka ac > bc
jika a < b dan c > 0, maka ac < bc
jika a > b dan c > 0, maka a/c > b/c
jika a < b dan c < 0, maka a/c < b/c
d. Jika kedua ruas persamaan dikalikan atau dibagi dengan bilangan
negatif yang sama, maka tanda atau notasi ketidaksamaannya
berubah atau dapat dituliskan sebagai berikut:
jika a > b dan c < 0, maka ac < bc
jika a < b dan c < 0, maka ac > bc
jika a > b dan c < 0, maka a/c < b/c
jika a < b dan c < 0, maka a/c > b/c
Pertidaksamaan Linier
Pertidaksamaan linier di definisikan sebagai pertidaksamaan
yang memuat variabel dengan pangkat tertinggi 1 (satu).untuk
menentukan penyelesaian persamaan linier digunakan sifat-sifat
yang berlaku pada pertidaksamaan. Agar kamu dapat memahaminya
perhatikan contoh berikut ini:
Contoh:
Tentukan himpunan penyelesaian dari pertidaksamaan berikut
dan gambarkan hasilnya pada garis bilangan!
4x + 3 < 2x - 5
Penyelesaian:
4x + 3 < 2x - 5
4x - 2x < -5 - 3
2x < -8
x < -8/2
x < -4
Jadi, himpunan penyelesaian nya adalah {x| -2 < -4, x elemen R}
Penerapan Pertidaksamaan Satu Variabel dalam Menyelesaikan Masalah
Banyak masalah dalam kehidupan sehari-hari dapat kita
selesaikan dengan menggunakan pertidaksamaan. Tahukah
kamu bagaimana menyelesaikan masalah tersebut dengan
menggunakan pertidaksamaan? Ada beberapa lankah yang
harus kita lakukan untuk menyelesaikan masalah dalam kehidupan
sehari-hari dengan menggunakan pertidaksamaan, yaitu:
1. Memodelkan masalah tersebut kedalam pertidaksamaan
2. Menyelesaikan model yang diperoleh pada langkah sebelumnya
3. Menafsirkan hasil yang di peroleh kedalam persamaan sebenarnya
Sekian yang dapat saya sampaikan pada artikel kali ini
semoga bermanfaat bagi pembaca dan penulis dan semoga
dapat membantu para pembaca dalam menyelesaikan
masalah dalam kehidupan sehari-hari dengan menggunakan pertidaksamaan.
Terimakasih.
Minggu, 31 Mei 2020
Garis Singgung Lingkaran
Pengertian Garis Singgung Lingkaran
Garis singgung lingkaran adalah garis yang apabila diperpanjang akan memotong lingkaran hanya pada satu titik. Titik potong garis singgung lingkaran dengan lingkaran disebut titik singgung.
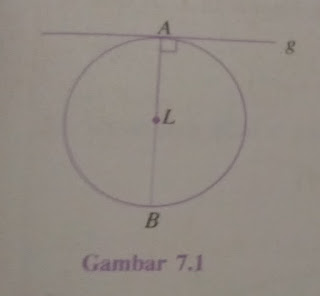
Garis singgung lingkaran selalu tegak lurus dengan jari-jari atau diameter yang melalui titik singgung. perhatikan gambar dibawah ini:
garis g adalah garis singgung lingkaran L dengan titik singgung A. Garis g tegak lurus dengan AL (jari-jari lingkaran). Garis g juga tegak lurus dengan AB (diameter lingkaran).
Sifat-sifat Garis Singgung Lingkaran
Sudut lancip antara garis singgung lingkaran dengan tali busur yang melalui titik singgung. sama dengan sudut keliling yang menghadap tali busur tersebut.
Perhatikan gambar 7.2. Garis FB menyinggung lingkaran L pada titik A, dan AD adalah diameter lingkaran L, maka
1. Melukis Garis Singgung Lingkaran Melalui Titik Singgung
Misal A adalah titik singgung yang terletak pada lingkaran L.
Langkah-langkah melukis garis singgung pada titik A.
(i) Lukislah jari-jari lingkaran L melalui A.
(ii) Lukislah garis BAC yang tegak lurus garis LA, dan berpotongan dititik A.
(iii) Garis BCA merupakan garis singgunglingkaran L (lihat gambar 7.6)
2. Melukis Garis Singgung Lingkaran Melalui Titik Di luar Lingkaran
Misal P adalah titik yang terletak diluar lingkaran L.
Langkah-langkah melukis garis singgung yang melalui titik P.
(i) Hubungkan titik P dan L
(ii) Carilah titik tengah PL (misal Q)
(iii) Buatlah lingkaran Q berjari-jari QP atau QL memotong lingkaran L di S dan T.
(iv) Hubungkan titik S dan T dengan titik P
(v) Garis PS dan PT adalah garis singgung lingkaran L (Lihat gambar 7.7)
Sekian yang dapat saya sampaikan dalam artikel kali ini,
semoga bermanfaat dan bisa membantu para pembaca
dalam menyelesaikan permasalahan atau soal tentang materi yang
saya lampirkan
Terimakasih.
Garis singgung lingkaran adalah garis yang apabila diperpanjang akan memotong lingkaran hanya pada satu titik. Titik potong garis singgung lingkaran dengan lingkaran disebut titik singgung.
Garis singgung lingkaran selalu tegak lurus dengan jari-jari atau diameter yang melalui titik singgung. perhatikan gambar dibawah ini:
Sifat-sifat Garis Singgung Lingkaran
- Garis singgung lingkaran memotong lingkaran hanya pada satu titik.
- Garis singgung lingkaran tegak lurus dengan jari-jari lingkaran pada titik singgung.
- Garis yang tegak lurus dengan garis singgung pada titik singgung pasti melalui titik pusat lingkaran.
- Garis yang tegak lurus dengan diameter dan melalui titik ujungnya adalah garis singgung.
Sudut lancip antara garis singgung lingkaran dengan tali busur yang melalui titik singgung. sama dengan sudut keliling yang menghadap tali busur tersebut.
Misal A adalah titik singgung yang terletak pada lingkaran L.
Langkah-langkah melukis garis singgung pada titik A.
(i) Lukislah jari-jari lingkaran L melalui A.
(ii) Lukislah garis BAC yang tegak lurus garis LA, dan berpotongan dititik A.
(iii) Garis BCA merupakan garis singgunglingkaran L (lihat gambar 7.6)
Misal P adalah titik yang terletak diluar lingkaran L.
(i) Hubungkan titik P dan L
(ii) Carilah titik tengah PL (misal Q)
(iii) Buatlah lingkaran Q berjari-jari QP atau QL memotong lingkaran L di S dan T.
(iv) Hubungkan titik S dan T dengan titik P
(v) Garis PS dan PT adalah garis singgung lingkaran L (Lihat gambar 7.7)
Sekian yang dapat saya sampaikan dalam artikel kali ini,
semoga bermanfaat dan bisa membantu para pembaca
dalam menyelesaikan permasalahan atau soal tentang materi yang
saya lampirkan
Terimakasih.
Selasa, 19 Mei 2020
RELASI DAN FUNGSI
Pengertian Relasi
Dalama kehidupan sehari-hari, banyak kita temukan hubungan, misalnya hubungan pertemuan, hubungan pekerjaan, dan hubungan kekeluargaan.
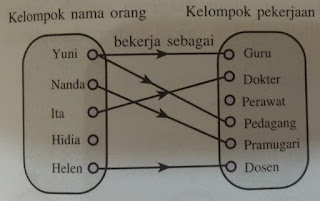
Kata hubungan dapat digunakan untuk menghubungkan dua kelompok (himpunan) dan hubungan tersebut memiliki sebuah "nama". Misalnya ada dua kelompok, yaitu kelompok nama oranng dan nama pekerjaan, lalu kedua kelompok tersebut kita hubungkan dengan nama hubungan "bekerja sebagai", seperti terlihat pada gambar dibawah ini;
Berdasarkan gambar diatas, kita dapat menyatakan hubungan berikut ini:
Yuni bekerja sebagai guru dan pedagang.
Nanda bekerja sebagai pramugari.
Ita bekerja sebagai dokter.
Helen bekerja sebagai dosen.
Hidia tidak mempunyai pekerjaan. digambarkan pada gambar berikut ini.
Jadi, suatu relasi dari kelompok A ke kelompok B adalah memasangkan anggota-anggota kelompok A dengan anggota kelompok B. Relasi dari A ke B dituliskan dengan R : A ---> B
Contoh:
Misalkan ada dua himpunan A dan B dengan
A = {1,4,9,14}
B = {1,2,3,4,5}
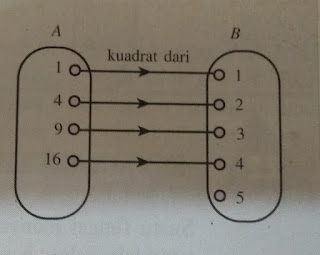
Relasi dari A ke B diberi nama kuadrat dari.
Relasi tersebut ini:
Pada relasi tersebut dapat kita nyatakan Hal-hal berikut:
1 adalah kuadrat dari 1
4 adalah kuadrat dari 2
9 adalah kuadrat dari 3
16 adalah kuadrat dari 4
5 tidak mempunyai pasangan
Definisi Fungsi
pernyataan sebuah fungsi diberikan berdasarkan kata-kata dalam kehidupan sehari-hari. Berikut ini diberikan pendefinisian fungsi secara matematis.
Anggap masing-masing unsur himpunan A dapat dipasangkan dengan tepat satu unsur di himpunan B. Pernyataan ini disebut sebuah fungsi. Jika perntyataan itu dinyatakan dengan f maka fungsi ditulis f : A---> B dan dibaca '' f adalah fungsi dari A ke B''.
Suatu fungsi dari himpunan A ke himpunan B adalah hubungan dari A ke B dimana untuk setiap x elemen A dipasangkan dengan tepat satu y elemen B. jika x elemen A, y elemen B, serta x dipasangkan dengan y, maka y dinamakan bayangan atau peta dari x, atau dapat juga dikatakan x dipetakan ke y dan dituliskan sebagai x ---> y. Himpunan y elemen B yang merupakan peta dari x elemen A disebut range atau daerah hasil fungsi. Himpunan x elemen A disebut domain dan semua anggota himpunan B disebut kodomain.
Notasi suatu Fungsi
Bila notasi fungsi diatas kita tuliskan dalam bentuk rumus fungsi ( formula fungsi) maka di peroleh:
Conth:
Tuliskan dalam bentuk notasi fungsi:
a. Nyatakan m = 6p^2 - p + 5 sebagai sebuah funsi dalam p.
b. Nyatakan luas L dari sebuah segitiga yang tingginya 10 meter sebagai sebuah fungsi dari alas a.
c. Nyatakan keliling K dari sebuah persegi panjang dengan lebar 8 cm sebagai sebuah fungsi dari panjang p.
Jawab:
a. Karena m adalah sebuah fungsi dari p, maka notasi fungsinya adalah : f(p) = 6p^2 - p + 5. untuk menyatakan m sebagai variabel bergantung , kita dapat juga menuliskannya sebagai m(p) = 6p^2 - p + 5.
b. Luas segitiga yang tingginya 10 meter ditentukan oleh formula :
L = 10a/2 atau L = 5a atau dapat juga ditulliskan dalam notasi fungsi:
f(a) = 5a atau L(a) = 5a
c Keliling persegi panjang dengan lebarr 8 cmditentukan oleh:
K = 2(p + 8) = 2p +16
Notasi fungsinya ditulis sebagai f(p) = 2p + 16 atau K(p) = 2p + 16
Sekian yang dapatsaya sampailkan dalam artikel kali ini,
semoga bermanfaat dan bisa membantu para pembaca
dalam memecahkan persoalan tentang relasi dan fungsi
Terimakasih.
Dalama kehidupan sehari-hari, banyak kita temukan hubungan, misalnya hubungan pertemuan, hubungan pekerjaan, dan hubungan kekeluargaan.
Kata hubungan dapat digunakan untuk menghubungkan dua kelompok (himpunan) dan hubungan tersebut memiliki sebuah "nama". Misalnya ada dua kelompok, yaitu kelompok nama oranng dan nama pekerjaan, lalu kedua kelompok tersebut kita hubungkan dengan nama hubungan "bekerja sebagai", seperti terlihat pada gambar dibawah ini;
Yuni bekerja sebagai guru dan pedagang.
Nanda bekerja sebagai pramugari.
Ita bekerja sebagai dokter.
Helen bekerja sebagai dosen.
Hidia tidak mempunyai pekerjaan. digambarkan pada gambar berikut ini.
Jadi, suatu relasi dari kelompok A ke kelompok B adalah memasangkan anggota-anggota kelompok A dengan anggota kelompok B. Relasi dari A ke B dituliskan dengan R : A ---> B
Contoh:
Misalkan ada dua himpunan A dan B dengan
A = {1,4,9,14}
B = {1,2,3,4,5}
Relasi dari A ke B diberi nama kuadrat dari.
Relasi tersebut ini:
1 adalah kuadrat dari 1
4 adalah kuadrat dari 2
9 adalah kuadrat dari 3
16 adalah kuadrat dari 4
5 tidak mempunyai pasangan
Definisi Fungsi
pernyataan sebuah fungsi diberikan berdasarkan kata-kata dalam kehidupan sehari-hari. Berikut ini diberikan pendefinisian fungsi secara matematis.
Anggap masing-masing unsur himpunan A dapat dipasangkan dengan tepat satu unsur di himpunan B. Pernyataan ini disebut sebuah fungsi. Jika perntyataan itu dinyatakan dengan f maka fungsi ditulis f : A---> B dan dibaca '' f adalah fungsi dari A ke B''.
Suatu fungsi dari himpunan A ke himpunan B adalah hubungan dari A ke B dimana untuk setiap x elemen A dipasangkan dengan tepat satu y elemen B. jika x elemen A, y elemen B, serta x dipasangkan dengan y, maka y dinamakan bayangan atau peta dari x, atau dapat juga dikatakan x dipetakan ke y dan dituliskan sebagai x ---> y. Himpunan y elemen B yang merupakan peta dari x elemen A disebut range atau daerah hasil fungsi. Himpunan x elemen A disebut domain dan semua anggota himpunan B disebut kodomain.
Notasi suatu Fungsi
- Misalkan fungsi A ke B kita sebut f maka notasi yang digunakan untuk menyatakan fungsi itu adalah:
- jika x elemen A, y elemen B, dan y adalah peta (bayangan) dari x maka notasi funsi di atas ditulis sebagai berikut:
Bila notasi fungsi diatas kita tuliskan dalam bentuk rumus fungsi ( formula fungsi) maka di peroleh:
Conth:
Tuliskan dalam bentuk notasi fungsi:
a. Nyatakan m = 6p^2 - p + 5 sebagai sebuah funsi dalam p.
b. Nyatakan luas L dari sebuah segitiga yang tingginya 10 meter sebagai sebuah fungsi dari alas a.
c. Nyatakan keliling K dari sebuah persegi panjang dengan lebar 8 cm sebagai sebuah fungsi dari panjang p.
Jawab:
a. Karena m adalah sebuah fungsi dari p, maka notasi fungsinya adalah : f(p) = 6p^2 - p + 5. untuk menyatakan m sebagai variabel bergantung , kita dapat juga menuliskannya sebagai m(p) = 6p^2 - p + 5.
b. Luas segitiga yang tingginya 10 meter ditentukan oleh formula :
L = 10a/2 atau L = 5a atau dapat juga ditulliskan dalam notasi fungsi:
f(a) = 5a atau L(a) = 5a
c Keliling persegi panjang dengan lebarr 8 cmditentukan oleh:
K = 2(p + 8) = 2p +16
Notasi fungsinya ditulis sebagai f(p) = 2p + 16 atau K(p) = 2p + 16
Sekian yang dapatsaya sampailkan dalam artikel kali ini,
semoga bermanfaat dan bisa membantu para pembaca
dalam memecahkan persoalan tentang relasi dan fungsi
Terimakasih.
Senin, 18 Mei 2020
Penerapan Bentuk Aljabar Dalam Kehidupan Sehari-hari
Laba (Untung) dan Rugi
1) Harga jual, harga beli, laba, dan rugi
Dalam berdagang, seseorang akan mmbeli suau barang dengan harga tertentu, yang disebut
harga beli, , kemudian dijualnya dengan harga tertentu yang disebut harga jual.
Bila seorang pedagang menjual barang dengan harga lebih tinggi dari harga beli maka dikatakan ia mendapatkan laba (untung). Sebaliknya, bila menjualnya dengan harga lebih rendah dari harga beli maka dikatakan rugi. Begitupun pula, bila harga jualnya sama dengan harga belinya maka dikatakan impas.
Dari uraian diatas, dapat disimpulkan sebagi berikut:
maka persamaan laba dan rugin dia atas diperoleh:
U = J - B R = B - J
J = B + U dan J = B - R
B = J - U B = J + R
Contoh 1:
Ayu membuet baju untuk di jual. Biaya pembuatan per potong Rp 70.000,00 karena jahitannya ada yang rusak, Ayu menjualnya dengan harga Rp 50.000,00 per potong. Apakah Ayu memperoleh untung rugi? Berapa untung atau ruginya? Penyelesaian:
harga beli baju per potong = Rp 70.000,00
harga jual baju per potong = Rp 50.000,00
Karena harga jual lebih rendah dari harga beli, berarti Ayu mengalami kerugian sehingga
kerugian yang dialami Ayu adalah:
Rugi = harga beli - harga jual
= Rp 70.000,00 - Rp 50.000,00
= Rp 20.000,00
Jadi, ayu mengalami kerugian sebesar Rp 20.000,00
contoh 2:
Iis membeli gula Rp 5.500,00 per kg, kemudian dijual dan mendapatkan untung Rp 500,00 per kg. Berapa harga jual per kg?
Penyelesaian:
Harga beli gula per kg =Rp 5.500,00
Untung gula per kg = Rp 500,00
Sehingga diperoleh:
Harga jual = harga beli + untung
= Rp 5.500,00 + Rp 500,00
= Rp 6.000,00
2). Menentuka presentase untung atau rugi dari harga beli
Kadang-kadang orang menyatakan untung dan rugi dalam bentuk persen, misalnya mendapat untung 20% atau rugi 6%. Untuk menyatakan presentase untung atau rugi, biasanya dari harga beli, tetapi ada juga yang dinyatakan dari harga jual. Namun, demikian bila tidak ada keterangan dari harga beli atau harga jualnya, berarti presentase untung atau ruginya dihitung dari harga beli.
Agar lebih jelasnya, mari kita perhatikan contoh berikut!
Contoh:
1. Pak surya membeli sepeda motor seharga Rp 10.000.000,00 dan dijual seharga Rp 12.000.000,00. Nyatakan untung atau rugi sebagai persen dari:
a. harga beli b. harga jual
Penyelesaian:
Karena harga jual lebih tinggi dari harga beli, maka untung.
besarnya untung = harga jual - harga beli
= Rp 12.000.000,00 - Rp 10.000.000,00
= Rp 2.000.000,00
Maka:
a. Untung yang di peroleh bila dinyatakan sebagai presentase dari harga beli adalah:
b. Untung yang diperoleh jika dinyatakan sebagai presentase dari harga jual adalah:
2. Ibu Lina membeli beras seharga Rp 4000,00 per kg, dan dijual seharga Rp 5.000,00 per kg. Berapa persen untung atau rugi yang diperoleh ibu Lina?
Penyelesaian:
karena harga jual lebih tinggi dari harga beli, berarti diperoleh untung (laba)
Besarnya untung = harga jual - harga beli
= Rp 5.000,00 - Rp 4.000,00
= Rp 1.000,00
Jadi untung yang diperoleh jika dinyatakan sebagai presentase adalah
sekian yang dapat saya sampaikan dalam artikel kali ini,
semoga bermanfaat dan bisa membantu para pembaca
dalam menyelesaikan permasalah mengenai materi yang telah saya tulis
Terimakasih.
1) Harga jual, harga beli, laba, dan rugi
Dalam berdagang, seseorang akan mmbeli suau barang dengan harga tertentu, yang disebut
harga beli, , kemudian dijualnya dengan harga tertentu yang disebut harga jual.
Bila seorang pedagang menjual barang dengan harga lebih tinggi dari harga beli maka dikatakan ia mendapatkan laba (untung). Sebaliknya, bila menjualnya dengan harga lebih rendah dari harga beli maka dikatakan rugi. Begitupun pula, bila harga jualnya sama dengan harga belinya maka dikatakan impas.
Dari uraian diatas, dapat disimpulkan sebagi berikut:
- Laba (Untung) diperoleh apabila harga jual lebih rendah dari harga beli. sehingga diperoleh rumus:
- Rugi diperoleh apabila harga jual lebih rendah dari harga beli. sehingga diperoleh rumus:
- Impas terjadi apabila harga jual sama dengan harga beli
maka persamaan laba dan rugin dia atas diperoleh:
U = J - B R = B - J
J = B + U dan J = B - R
B = J - U B = J + R
Contoh 1:
Ayu membuet baju untuk di jual. Biaya pembuatan per potong Rp 70.000,00 karena jahitannya ada yang rusak, Ayu menjualnya dengan harga Rp 50.000,00 per potong. Apakah Ayu memperoleh untung rugi? Berapa untung atau ruginya? Penyelesaian:
harga beli baju per potong = Rp 70.000,00
harga jual baju per potong = Rp 50.000,00
Karena harga jual lebih rendah dari harga beli, berarti Ayu mengalami kerugian sehingga
kerugian yang dialami Ayu adalah:
Rugi = harga beli - harga jual
= Rp 70.000,00 - Rp 50.000,00
= Rp 20.000,00
Jadi, ayu mengalami kerugian sebesar Rp 20.000,00
contoh 2:
Iis membeli gula Rp 5.500,00 per kg, kemudian dijual dan mendapatkan untung Rp 500,00 per kg. Berapa harga jual per kg?
Penyelesaian:
Harga beli gula per kg =Rp 5.500,00
Untung gula per kg = Rp 500,00
Sehingga diperoleh:
Harga jual = harga beli + untung
= Rp 5.500,00 + Rp 500,00
= Rp 6.000,00
2). Menentuka presentase untung atau rugi dari harga beli
Kadang-kadang orang menyatakan untung dan rugi dalam bentuk persen, misalnya mendapat untung 20% atau rugi 6%. Untuk menyatakan presentase untung atau rugi, biasanya dari harga beli, tetapi ada juga yang dinyatakan dari harga jual. Namun, demikian bila tidak ada keterangan dari harga beli atau harga jualnya, berarti presentase untung atau ruginya dihitung dari harga beli.
Agar lebih jelasnya, mari kita perhatikan contoh berikut!
Contoh:
1. Pak surya membeli sepeda motor seharga Rp 10.000.000,00 dan dijual seharga Rp 12.000.000,00. Nyatakan untung atau rugi sebagai persen dari:
a. harga beli b. harga jual
Penyelesaian:
Karena harga jual lebih tinggi dari harga beli, maka untung.
besarnya untung = harga jual - harga beli
= Rp 12.000.000,00 - Rp 10.000.000,00
= Rp 2.000.000,00
Maka:
a. Untung yang di peroleh bila dinyatakan sebagai presentase dari harga beli adalah:
b. Untung yang diperoleh jika dinyatakan sebagai presentase dari harga jual adalah:
2. Ibu Lina membeli beras seharga Rp 4000,00 per kg, dan dijual seharga Rp 5.000,00 per kg. Berapa persen untung atau rugi yang diperoleh ibu Lina?
Penyelesaian:
karena harga jual lebih tinggi dari harga beli, berarti diperoleh untung (laba)
Besarnya untung = harga jual - harga beli
= Rp 5.000,00 - Rp 4.000,00
= Rp 1.000,00
Jadi untung yang diperoleh jika dinyatakan sebagai presentase adalah
sekian yang dapat saya sampaikan dalam artikel kali ini,
semoga bermanfaat dan bisa membantu para pembaca
dalam menyelesaikan permasalah mengenai materi yang telah saya tulis
Terimakasih.
Selasa, 21 April 2020
Bilangan Biner
Pengertian Bilangan Biner
Pada kesempatan kali ini kita akan mengulas sedikit tentang bagian dari bilangan-bilangan yang ada dalam matematika, taitu bilangan biner.
Bilangan biner merupakan sistem bilangan berbasis 2 yang mana penulisnya menggukana dua simbol angka, yaitu 0 dan 1.
Sistem bilangan biner modren pertama kali ditemukan oleh Gottfried Wilhelm Leibniz pada abad ke-17.
istila bilangan biner kerap disebut juga dengangan bit, atau digit biner.
dalam penggunaanya, baianya bilangan biner digunakan pada bidang digital atau segala sesuatu yang membutuhkan pernyataan "ya" dan " tidak", "diaktifkan" dan "mati", serta "buka" dan "tutup".
Misalnya saja penggunaanya pada tombol power komputer. Penggunaanya cukup muda pada aplikasi membuat bilangan biner dipilih dalam hal ini.
setelah kita tahu apa itu bilangan biner atau bit, selanjutnya kita akan bahas tentang cara penghitungan bilangan biner.
Penghitungan bilangan biner dapat disetujui cukup sederhana. Pada istilah komputer, biner slalu menghitung 8 dengan istilah i byte.
Pada sistem pengkodean 1 byte mana yang dimiliki 8 bit ini hanya memiliki angka 0 dan 1 pada penghitungannya.
Berikut contoh penghitungan bilangan biner pada sistem cooding 1 bite.
Perhatikan pola yang ada pada tabel diatas.Dalam penghitungannya, bilangan biner dimulai dari 0000000 untuk siste bilangan biner 8 bit (1 byte).
Selanjutnya perhitungan ini melampaui angka 11111111. Setelah ini, kita akan membahas tentang penjumlahan dari bilanagn biner.
Penjumlahan Bilangan Biner
Operasi penjumlahan pada bilanga biner memiliki 4 persyaratan yang perlu disetujui di bawah ini.
0 + 0 = 0
1 + 0 = 1
0 + 1 = 1
1 + 1 = 0 (melaksanakan 1)
Makssud dari melaksanakan diatas adalah menyimpan sejumlah nilai dan akan dimasukkan / subsitusi ke nilai di sebelahnya yang lebih besar.
Hubungi contoh di bawah ini (penjumlahan bilangan biner 8 bit):
buktikan 8 + 11 = 19 menggunakan operasi penjumlahan bilangan biner!
Pada contoh diatas, dilakukan pada saat 1 + 1 = 0 dengan melaksanakan 1 dan dibawah subsitusi nilai tambah yang lebih tinggi sehingga 1 + 0 + 0 = 1.
Pengurangan Bilangan Biner
Untuk operasi memilih bilangan biner, 4 hal yang harus diperhatikan adalah sebagai berikut:
buktikan 19 - 11= 8 menggunakan operasi bilangan biner:
Demikian pembahasan saya tentang bilangan biner
semoga bisa membantu pembaca dalam menyelesaikan masalah tentang bilangan biner, dan semoga bermanfat bagi semua nya.........
Pada kesempatan kali ini kita akan mengulas sedikit tentang bagian dari bilangan-bilangan yang ada dalam matematika, taitu bilangan biner.
Bilangan biner merupakan sistem bilangan berbasis 2 yang mana penulisnya menggukana dua simbol angka, yaitu 0 dan 1.
Sistem bilangan biner modren pertama kali ditemukan oleh Gottfried Wilhelm Leibniz pada abad ke-17.
istila bilangan biner kerap disebut juga dengangan bit, atau digit biner.
dalam penggunaanya, baianya bilangan biner digunakan pada bidang digital atau segala sesuatu yang membutuhkan pernyataan "ya" dan " tidak", "diaktifkan" dan "mati", serta "buka" dan "tutup".
Misalnya saja penggunaanya pada tombol power komputer. Penggunaanya cukup muda pada aplikasi membuat bilangan biner dipilih dalam hal ini.
setelah kita tahu apa itu bilangan biner atau bit, selanjutnya kita akan bahas tentang cara penghitungan bilangan biner.
Penghitungan bilangan biner dapat disetujui cukup sederhana. Pada istilah komputer, biner slalu menghitung 8 dengan istilah i byte.
Pada sistem pengkodean 1 byte mana yang dimiliki 8 bit ini hanya memiliki angka 0 dan 1 pada penghitungannya.
Berikut contoh penghitungan bilangan biner pada sistem cooding 1 bite.
Perhatikan pola yang ada pada tabel diatas.Dalam penghitungannya, bilangan biner dimulai dari 0000000 untuk siste bilangan biner 8 bit (1 byte).
Selanjutnya perhitungan ini melampaui angka 11111111. Setelah ini, kita akan membahas tentang penjumlahan dari bilanagn biner.
Penjumlahan Bilangan Biner
Operasi penjumlahan pada bilanga biner memiliki 4 persyaratan yang perlu disetujui di bawah ini.
0 + 0 = 0
1 + 0 = 1
0 + 1 = 1
1 + 1 = 0 (melaksanakan 1)
Makssud dari melaksanakan diatas adalah menyimpan sejumlah nilai dan akan dimasukkan / subsitusi ke nilai di sebelahnya yang lebih besar.
Hubungi contoh di bawah ini (penjumlahan bilangan biner 8 bit):
buktikan 8 + 11 = 19 menggunakan operasi penjumlahan bilangan biner!
Pengurangan Bilangan Biner
Untuk operasi memilih bilangan biner, 4 hal yang harus diperhatikan adalah sebagai berikut:
buktikan 19 - 11= 8 menggunakan operasi bilangan biner:
Demikian pembahasan saya tentang bilangan biner
semoga bisa membantu pembaca dalam menyelesaikan masalah tentang bilangan biner, dan semoga bermanfat bagi semua nya.........
Senin, 20 April 2020
Fungsi Rasional
Pengertian Fungsi Rasional
Fungsi rasional adalah fungsi yang dapat didefinisikan dengan fraksi rasional dalam fraksi al jabar sehingga pembilang dan penyebutnya adalah polinominal.
Sebuah fungsi f(x) disebut fungsi rasional jika dan hanya jika fungsi tersebutn dapat ditulis dalam bentuk.
dimana P dan Q adalah polinominal dari x dan Q bukan fungsi nol. Domain dari f adalah himpunana semua nilai x untuk yang penyebutnya Q(x) bukan nol.
Namun jika P dan Q memiliki pembagi umum terbesar polinomial non-konstanta R, lalu P = P1R dan Q = Q1 R menghasilkan fungsi rasional.
yang mugkin memiliki domain lebih besar dari f(x), dan sama dengan f(x) pada domain f(x). Bentuk ini umumnyadigunakan untuk memperluas " kontinuitas" domain f(x) untuk f1(x).
Fungsi rasional yang tepat adalah fungsi rasional dimana derajat P tidak lebih besar dari derajat Q dan keduanya polinomial nyata.
Contoh:
Examples of rational functions
Fungsi rasional
tidak didefinisikan sebagai
Fungsi rasional
didefinisikan untuk semua bilangan riil, tetapi tidak untuk semua bilangan kompleks, karena jika x merupakan akar kuadrad dari -1 ( bilangan imajiner atau negatifnya), maka perhitungannya normal akan mengarah kepada pembagian nol:
yang tidak terdefinisi.
Fungsi konstanta seperti f(x) = fii, adalah fungsi rasional karena konstanta merupakan polinomial. Fungsi itu sendiri merupakan rasional meskipun nilai dari f(x) tidak rasional untuk semua x.
Untuk setiap fungsi polinom f(x) = P(x) adalah funsi rasional dengan Q(x) = 1. Fungsi yang tidak dapat ditulis dalam bentuk ini, seperti f(x) = sin (x), bukan merupakan fungsi rasional. kata sifat "irasional" umumnya tidak digunakan untuk fungsi.
Fungsi rasional f(x) = x/x sama dengan 1 untuk semua x kecuali 0. Jumlah, produk, atau hasil bagi ( kecuali pembagian dengan polinomial nol) dari dua funsi rasional itu sendiri adalah funsi rasional. Namun, proses reduksi ke bentuk standar dapat secara tidak sengaja menghasilkan penghapusan singularitas seperti itu kecualidilakukan perawatan.
Cukup sekian yang dapat saya sampaikan dalam artikel ini semoga bermanfaat bagi semuanya yang sudah membaca nya
Dan terimakasih sudah membaca
Fungsi rasional adalah fungsi yang dapat didefinisikan dengan fraksi rasional dalam fraksi al jabar sehingga pembilang dan penyebutnya adalah polinominal.
Sebuah fungsi f(x) disebut fungsi rasional jika dan hanya jika fungsi tersebutn dapat ditulis dalam bentuk.
Namun jika P dan Q memiliki pembagi umum terbesar polinomial non-konstanta R, lalu P = P1R dan Q = Q1 R menghasilkan fungsi rasional.
Fungsi rasional yang tepat adalah fungsi rasional dimana derajat P tidak lebih besar dari derajat Q dan keduanya polinomial nyata.
Contoh:
Examples of rational functions
Fungsi rasional
Fungsi konstanta seperti f(x) = fii, adalah fungsi rasional karena konstanta merupakan polinomial. Fungsi itu sendiri merupakan rasional meskipun nilai dari f(x) tidak rasional untuk semua x.
Untuk setiap fungsi polinom f(x) = P(x) adalah funsi rasional dengan Q(x) = 1. Fungsi yang tidak dapat ditulis dalam bentuk ini, seperti f(x) = sin (x), bukan merupakan fungsi rasional. kata sifat "irasional" umumnya tidak digunakan untuk fungsi.
Fungsi rasional f(x) = x/x sama dengan 1 untuk semua x kecuali 0. Jumlah, produk, atau hasil bagi ( kecuali pembagian dengan polinomial nol) dari dua funsi rasional itu sendiri adalah funsi rasional. Namun, proses reduksi ke bentuk standar dapat secara tidak sengaja menghasilkan penghapusan singularitas seperti itu kecualidilakukan perawatan.
Cukup sekian yang dapat saya sampaikan dalam artikel ini semoga bermanfaat bagi semuanya yang sudah membaca nya
Dan terimakasih sudah membaca
Sabtu, 18 April 2020
Koordinat Kartesius
Pengertian koordinat kartesius
Taukah kalian? kata ' kartesius 'nmerupakan latinisasi untuk 'Descartes ' yang juga merupakan nama dari seorang ahli matematika dari prancis yang mengumpulkan banyak cabang ilmu matematika yaitu geometri dan aljabar.
Ide dasar pengetahuan ini ada dalam buku Descartes " Wacana tentang metode" di dalam buku tersebut, Descartes memperkenalkan metode untuk menggambarkan posisi dari sebuah titik dengan menggunakan dua poros yang saling tegak lurus, yang dibuka sekarang kita kenal dangan kartesius.
koordinat kartesius digunakan untuk menentukan posisi dari titik dalam didang menggunakan pasangan bilangan yang disebut dengan absis (koordinat x) dan ordinat (koordinat) dari titik tersebut.
Dalam menentukan koordinat satu titik diperlukan dua sumbuh yang saling tegak lurus (sumbu x dan sumbu y) dan satuan panjang, yang memiliki tanda pada kedua ujung sumbu tersebut lebih jelasnya lihat gambar dibawah ini.
Siste koordinat kartesius ini dapat digunakan pada dimensi 3 yang menggunakan 3 sumbu, yaitu sumbu x, sumbu y, dan sumbu z.
Diagram Kartesius
pada materi ini hanya akan dibahas diagram kartesius untuk sistem koordinat kartesius dus dimensi saja.
sistem koordinat dua dimensi ditentukan dengan dua sumbu yang saling tegak lurus dan diletakkan pada satu bidang xy.
lebel diberi vertikal sumbu y dan label horizontal x. kedua sumbuh ini saling berpotongan pada titik yang kemudian diberi label o.
Setiap sumbu memiliki satuan panjang yang ditandai dan kemudian disusun sesuai kisi.
Notasi dalam menyatakan sebuah titik adalah (x, y)dimana x menyatakan nilai terhadap sumbu x (abssi) dan y menyatakan nilai terhadap sumbu y (ordinat), sehingga urutan x dan y dalam (x, y) tidak dapat dibalik-balik.
karena sumbu x dan sumbu y saling tegak lurus maka bidang xy kemudian terbagi menjadi 4 bagian (kuadran) yaitu kuadran l,ll,ll,lv yang berurutan melawan arah jarum jam dan mulai dari kanan atas. lebih jelasnya ada pada gambar dibawah ini.
sesuai dengan kuadradnya, kuadran aku punya absis dan ordinat yang sama-sama bernilai positif.
kuadran dua absisnya bernilai negatif sengakan ordinatnya bernilai positif.
kuadran tiga memiliki absis dan ordinat bernilai negatif .
kuadran empat absis bernilai positif dan ordinat bernilai negatif.
contoh soal koordinat kartesius
berlokasi di kuadran berapakah titik-titik di bawah ini
1 (2,3)
2 (3,3)
3 (-4,7)
4 (85,-77)
5 (-54,2)
Penyelesaian
1 (2,3) Berlokasi pada kuadran l
2 (3,3) Berlokasi pada kuadran l
3(-4,7) Berlokasi pada kuadran ll
4 (85,-77) Berlokasi pada kuadran lv
5 (-54,2) Berlokasi pada kuadran lll
Demikian pembahasan yang dapat saya sampaikan pada artikel kali ini
semoga bermanfaat bagi semua pembaca
Taukah kalian? kata ' kartesius 'nmerupakan latinisasi untuk 'Descartes ' yang juga merupakan nama dari seorang ahli matematika dari prancis yang mengumpulkan banyak cabang ilmu matematika yaitu geometri dan aljabar.
Ide dasar pengetahuan ini ada dalam buku Descartes " Wacana tentang metode" di dalam buku tersebut, Descartes memperkenalkan metode untuk menggambarkan posisi dari sebuah titik dengan menggunakan dua poros yang saling tegak lurus, yang dibuka sekarang kita kenal dangan kartesius.
koordinat kartesius digunakan untuk menentukan posisi dari titik dalam didang menggunakan pasangan bilangan yang disebut dengan absis (koordinat x) dan ordinat (koordinat) dari titik tersebut.
Dalam menentukan koordinat satu titik diperlukan dua sumbuh yang saling tegak lurus (sumbu x dan sumbu y) dan satuan panjang, yang memiliki tanda pada kedua ujung sumbu tersebut lebih jelasnya lihat gambar dibawah ini.
Siste koordinat kartesius ini dapat digunakan pada dimensi 3 yang menggunakan 3 sumbu, yaitu sumbu x, sumbu y, dan sumbu z.
Diagram Kartesius
pada materi ini hanya akan dibahas diagram kartesius untuk sistem koordinat kartesius dus dimensi saja.
sistem koordinat dua dimensi ditentukan dengan dua sumbu yang saling tegak lurus dan diletakkan pada satu bidang xy.
lebel diberi vertikal sumbu y dan label horizontal x. kedua sumbuh ini saling berpotongan pada titik yang kemudian diberi label o.
Setiap sumbu memiliki satuan panjang yang ditandai dan kemudian disusun sesuai kisi.
Notasi dalam menyatakan sebuah titik adalah (x, y)dimana x menyatakan nilai terhadap sumbu x (abssi) dan y menyatakan nilai terhadap sumbu y (ordinat), sehingga urutan x dan y dalam (x, y) tidak dapat dibalik-balik.
karena sumbu x dan sumbu y saling tegak lurus maka bidang xy kemudian terbagi menjadi 4 bagian (kuadran) yaitu kuadran l,ll,ll,lv yang berurutan melawan arah jarum jam dan mulai dari kanan atas. lebih jelasnya ada pada gambar dibawah ini.
sesuai dengan kuadradnya, kuadran aku punya absis dan ordinat yang sama-sama bernilai positif.
kuadran dua absisnya bernilai negatif sengakan ordinatnya bernilai positif.
kuadran tiga memiliki absis dan ordinat bernilai negatif .
kuadran empat absis bernilai positif dan ordinat bernilai negatif.
contoh soal koordinat kartesius
berlokasi di kuadran berapakah titik-titik di bawah ini
1 (2,3)
2 (3,3)
3 (-4,7)
4 (85,-77)
5 (-54,2)
Penyelesaian
1 (2,3) Berlokasi pada kuadran l
2 (3,3) Berlokasi pada kuadran l
3(-4,7) Berlokasi pada kuadran ll
4 (85,-77) Berlokasi pada kuadran lv
5 (-54,2) Berlokasi pada kuadran lll
Demikian pembahasan yang dapat saya sampaikan pada artikel kali ini
semoga bermanfaat bagi semua pembaca
Jumat, 17 April 2020
Simpangan Rata Rata
Pengertaian Simpangan Rata Rata
Simpangan rata rata merupakan termasuk kedalam ukuran penyebaran data seperti halnya Varian dan Standar Deviasi. kegunaannya adalah untuk mengetahui seberapa jauh nilai data yang telah menyimpang dari rata-rata yang sebenarnya.
Rumus Simpangan Rata-Rata
sekumpulan data kuantitatif yang tidak dikelompokkan serta dinyatakan oleh x1,x2,....xn. Dari data tersebut dapat ditentukan simpangan rata-rata (Sr) dengan menggunakan sebuah rumus sebagai berikut:
contoh soal 1
Hitunglah simpangan rata-rata dari data kuatitatif tersebut
12,3,11,3,4,7,5,11
Pembahasan
Maka, simpangan rata-ratanya adalah 3,25
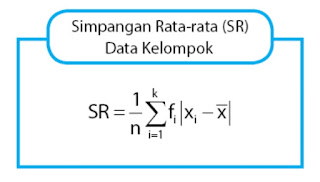
Untuk sekumpulan data yang dinyatakan oleh x1,x2,......,xn dan amsing-masing nilai data tersebut mempunyai frekuensi f1,f2,..., fn maka diperoleh nilai simpangan rata-rata menggunakan rumus:
contoh soal 2
Hitunglah simpangan rata-rata nilai ulangan Matematika siswa Kelas XI MAN 2 Merdeka seperti Tabel 1 dibawah berikut:
Tabel 1. Nilai ulanagan Matematika siswa kelas XI MAN 2 Merdeka
penyelesaian:
Dari tabel diatas, diperoleh = 65,7 (dibulatkan)
Maka, simpangan rata-rata = 671,7/71= 9,46simpangan rataan hitung tersebjut menunjukkan rataan hitung jauhnya datum dari rataan hitung.
untuk menghitung simpangan baku dari data kuantitatif: 2,5,7,4,3,11,3 dengan kalkulator ilmiah (fx-3600Pv) ialah sebagai berikut:
Selanjutnya yaitu membahas simpangan rata-rata yang dibagi menjadi dua:
1. Simpangan Rata-Rata dengan Data Tunggal
Rumus Varian S^2 dari data tunggal
Rumus varian /ragam dari data tunggal ialah yang dinyatakan melalui persamaan dibawah berikut:
keterangan:
Rumus Standar Deviasi/Simpangan bakunya data tunggal ialah:
Rumus simpangan baku dan tunggal dinyatakan melalui sebuah persamaan dibawah ini
keterangan:
2. Simpangan Rata-Rata data berkelompok
runus:
keterangan:
Variasi (Ragam)
Persamaan untuk ragam atau variasi diberikan rumus sebagai berikut:
Standar Deviasi ( simpangan baku)
Rumus:
keterangan:
contoh soal dan pembahasannya
Diketahui sebuah data terurut (3x - 3), 2x,(2x + 1), (3x - 1), (3x + 3), dan (4x + 1). Jangkauan data tersebut ialah 6. Simpangan rata-rata dat tersebut yaitu.....
Pembahasannya:
Diketahui sebuah data berurut ialah sebagai berikut:
(3x -3), 2x (2x + 1), (3x -1), (3x +3), (4x + 1)
Nilai minimum =Xmin = 3x - 3
Nilai maksimum = X max + 4x + 1
jangkauan = Xmax- Xmin
6 = 4x +1 - (3x -3)
6 = 4x + 1 - 3x + 3
6 = x + 4
x = 2
Maka, daftar nilainya yaitu:
(3x - 3) = 3.2 -3 = 6 - 3= 3
2x = 2.2 = 4
2x + 1 = 2.2 + 1= 4 + 1= 5
3x - 1 = 3.2 -1 = 6 - 1 = 5
3x + 3 = 3.2 +3 = 6 + 3= 9
4x + 1 = 4.2 + 1 = 8 + 1 = 9
Maka, daftar nilainya yaitu:
(3x - 3) = 3.2 - 3 = 6 -3 = 3
2x = 2.2 = 4
2x + 1= 2.2 + 1 = 4 +1 = 5
3x -1 = 3.2 -1 = 6 - 1 = 5
3x + 3 = 3.3 + 3 = 6 + 3 = 9
4x + 1 = 4.2 + 1 = 8 + 1 = 9
oleh karena itu diperoleh data 3,4,5,5,7,9,9,
mencari rata-ratanya adalah:
mencari simpangan rata-ratanya ialah
Mungkin cukup sampai disini yang dapat saya jelaskan pada artikel ini
semoga bermanfaat iya bagi pembaca semua.
Simpangan rata rata merupakan termasuk kedalam ukuran penyebaran data seperti halnya Varian dan Standar Deviasi. kegunaannya adalah untuk mengetahui seberapa jauh nilai data yang telah menyimpang dari rata-rata yang sebenarnya.
Rumus Simpangan Rata-Rata
sekumpulan data kuantitatif yang tidak dikelompokkan serta dinyatakan oleh x1,x2,....xn. Dari data tersebut dapat ditentukan simpangan rata-rata (Sr) dengan menggunakan sebuah rumus sebagai berikut:
Hitunglah simpangan rata-rata dari data kuatitatif tersebut
12,3,11,3,4,7,5,11
Pembahasan
Maka, simpangan rata-ratanya adalah 3,25
Untuk sekumpulan data yang dinyatakan oleh x1,x2,......,xn dan amsing-masing nilai data tersebut mempunyai frekuensi f1,f2,..., fn maka diperoleh nilai simpangan rata-rata menggunakan rumus:
contoh soal 2
Hitunglah simpangan rata-rata nilai ulangan Matematika siswa Kelas XI MAN 2 Merdeka seperti Tabel 1 dibawah berikut:
Tabel 1. Nilai ulanagan Matematika siswa kelas XI MAN 2 Merdeka
Dari tabel diatas, diperoleh = 65,7 (dibulatkan)
untuk menghitung simpangan baku dari data kuantitatif: 2,5,7,4,3,11,3 dengan kalkulator ilmiah (fx-3600Pv) ialah sebagai berikut:
1. Simpangan Rata-Rata dengan Data Tunggal
Rumus Varian S^2 dari data tunggal
Rumus varian /ragam dari data tunggal ialah yang dinyatakan melalui persamaan dibawah berikut:
Rumus simpangan baku dan tunggal dinyatakan melalui sebuah persamaan dibawah ini
runus:
Persamaan untuk ragam atau variasi diberikan rumus sebagai berikut:
Rumus:
Diketahui sebuah data terurut (3x - 3), 2x,(2x + 1), (3x - 1), (3x + 3), dan (4x + 1). Jangkauan data tersebut ialah 6. Simpangan rata-rata dat tersebut yaitu.....
Pembahasannya:
Diketahui sebuah data berurut ialah sebagai berikut:
(3x -3), 2x (2x + 1), (3x -1), (3x +3), (4x + 1)
Nilai minimum =Xmin = 3x - 3
Nilai maksimum = X max + 4x + 1
jangkauan = Xmax- Xmin
6 = 4x +1 - (3x -3)
6 = 4x + 1 - 3x + 3
6 = x + 4
x = 2
Maka, daftar nilainya yaitu:
(3x - 3) = 3.2 -3 = 6 - 3= 3
2x = 2.2 = 4
2x + 1 = 2.2 + 1= 4 + 1= 5
3x - 1 = 3.2 -1 = 6 - 1 = 5
3x + 3 = 3.2 +3 = 6 + 3= 9
4x + 1 = 4.2 + 1 = 8 + 1 = 9
Maka, daftar nilainya yaitu:
(3x - 3) = 3.2 - 3 = 6 -3 = 3
2x = 2.2 = 4
2x + 1= 2.2 + 1 = 4 +1 = 5
3x -1 = 3.2 -1 = 6 - 1 = 5
3x + 3 = 3.3 + 3 = 6 + 3 = 9
4x + 1 = 4.2 + 1 = 8 + 1 = 9
oleh karena itu diperoleh data 3,4,5,5,7,9,9,
mencari rata-ratanya adalah:
semoga bermanfaat iya bagi pembaca semua.
Kamis, 16 April 2020
EKSPONEN
Pengertian Eksponen
Eksponen adalah bentuk perkalian suatu bilangan yang sama secara berulang-ulang. mungkin Quipperian biasa mendengar istilahnya sebagai bilangan berpangkat. contohnya sebagai berikut.
Bentuk eksponen bisa dinyatakan dalam bentuk persamaan maupun pertidaksamaan. Hal itu berkaitan dengan jenis penggunaanya, misalnya untuk menyelasaikan masalah yang berkaitan dengan fungsi eksponen.Nah, konsep dasar perkalian berulang-ulang inilah yang nantinya digunakan pemerintah untuk menghitung jumlah penduduk beberapa tahun ke depan. Tentunya dengan perhitungan dan penurunan rumus yang tidak mudah ya!
Persamaan Eksponen
persamaan eksponen adalah persamaan yang memiliki variabel bagian eksponennya. Secara umum, persamaan eksponen dibagi menjadi tiga bagian, yaitu persamaan eksponen berbasis konstanta, persamaan eksponen berbasis fungsi, dan persamaan eksponen dalam bentuk penjumlahan. Untuk penjelasan lebih lanjut, simak ulasan berikut:
1. Persamaan eksponen berbasis konstanta
untuk persamaan eksponen berbasis konstanta, terdapat dua persamaan yang harus dipahami,yaitu sebagai berikut.
untuk lebih jelasnya, simak contoh soal berikut ini,
contoh soal 1
pembahasan
untuk menentukan solusinya, harus menyamakan baris kedua ruas terlebih dahulu. Berdasarkan sifat-sifat eksponen, diperoleh:
jadi solusi dari persamaan diatas adalah x= 6
2. Persamaan eksponen berbasis fungsi
Bentuk umum persamaan eksponen di atas memiliki empat kemungkinan solusi, yaitu sebagai berikut.
a. g(x) = h(x)
b. f(x) = 1
c. f(x) = -1, dengan syarat g(x) dan h(x) sama-sama genap atau ganjil
d. f(x) = 0, dengan syarat g(x),h(x) >0
contoh soal 2
pembahasan
solusi dari oersamaan eksponen diatas, didapat dari 4 kondisi berikut.
uji pangakat untuk rusa kiri
uji pangkat untuk ruas kanan
x + 4 = 1 + 4 = 5 ( ganjil)
oleh karena sama-sama ganjil, maka x =1 merupakan penyelesaian
uji pangkat ruas kiri
oleh karena 0 bukan bilangan positif, maka x = 2 bukan termasuk penyelesaian.
jadi, himpunan penyelesaian dari persamaan eksponen dia tas adalah {-1,1,3,4}
3. Persamaan eksponen dalam bentuk penjumlahan
Bentuk umum persamaan eksponen penjumlahan adalah sebagai berikut.
Lalu bagaimana langkah-langkah menentukan hasil persamaan eksponen dalam bentuk penjumlahan ini?
a. Bentuk eksponen harunya di uraikan samapai diperoleh bentuk yang sama. Untuk mrnguraikannya, gunakan sifat-sifat berikut
b. gunakan permisalannya bentuk eksponen yang sama dengan variabel tertentu.
c. Selesaikan persamaanya, lalu subsitsikan kembali nilai variabel yang diperoleh pada permisalan.
untuk lebih jelasnya, simak contoh soal beerikut
contoh soal 3
tentukan solusi dari persamaan eksponen
pembahasan
misalnya 2^x = y, sehingga diperoleh:
Subsitusikan nilai balik y pada permisalan tersebut.
Jadi, solusi dari persamaan di atas adalah x = 3
Pertidaksamaan Eksponen
Pertidaksamaan Eksponen adalah pertidaksamaan jenis eksponen ysng memiliki variabel. Ternyata, pertidaksamaan eksponen memiliki dua bentuk umum yaitu sebagai berikut
:
untuk menentukan solusi pertidaksamaan di atas, ikuti langkah berikut.
1. bentuk eksponen harus diuraikan sampai diperoleh bentuk yang sama. uraikan berdasarkan sifat-sifat ekspinen.
2. Gunakan permisalan bentuk eksponen dengan variabel tertentu
3. Selesaikan pertidaksamaannya menggunakan konsep pertidaksamaan sampai diperoleh interval untuk permisalannya
4. Substitusikan nilai yang baik yang diperoleh pada permisalan.
Agar tambah paham dengan pertidaksamaan eksponen, perhatikan contoh berikut.
contoh soal 4
Tentukan himpunan penyelesaian dari pertidaksamaan eksponen
Pembahasan
untuk menentukan solusinya, harus menyamakan baris pada kedua ruas. Bertdasarkan eksponen diperoleh:
oleh karena a =7>1, maka berlaku:
Titik pembuat nol x = 4 dan x = 2
Selanjutnya, harus menempatkan titik pembuat nol dalam garis bilangan. Kemudian, tentukan tanda daerahnya dengan titik uji. Oleh karena tanda pertidaksamaannya "<", maka bulatannya kosong dan titik pembuat nol tidak termasuk dalam nilai x.
Jadi, Himpunan penyelesaian dari pertidaksamaan eksponen di atas adalah {x| x E R, 2 < x < 4}
sekian yang dapat saya sampaikan dalam blog ini semoga bermanfaat bagi pemca iya
sekian terima kasih
Eksponen adalah bentuk perkalian suatu bilangan yang sama secara berulang-ulang. mungkin Quipperian biasa mendengar istilahnya sebagai bilangan berpangkat. contohnya sebagai berikut.
Persamaan Eksponen
1. Persamaan eksponen berbasis konstanta
untuk persamaan eksponen berbasis konstanta, terdapat dua persamaan yang harus dipahami,yaitu sebagai berikut.
contoh soal 1
pembahasan
untuk menentukan solusinya, harus menyamakan baris kedua ruas terlebih dahulu. Berdasarkan sifat-sifat eksponen, diperoleh:
2. Persamaan eksponen berbasis fungsi
Bentuk umum persamaan eksponen di atas memiliki empat kemungkinan solusi, yaitu sebagai berikut.
b. f(x) = 1
c. f(x) = -1, dengan syarat g(x) dan h(x) sama-sama genap atau ganjil
d. f(x) = 0, dengan syarat g(x),h(x) >0
contoh soal 2
pembahasan
solusi dari oersamaan eksponen diatas, didapat dari 4 kondisi berikut.
- solusi ke-1
- solusi ke-2
- solusi ke-3
uji pangakat untuk rusa kiri
uji pangkat untuk ruas kanan
x + 4 = 1 + 4 = 5 ( ganjil)
oleh karena sama-sama ganjil, maka x =1 merupakan penyelesaian
- solusi ke-4
uji pangkat ruas kiri
oleh karena 0 bukan bilangan positif, maka x = 2 bukan termasuk penyelesaian.
jadi, himpunan penyelesaian dari persamaan eksponen dia tas adalah {-1,1,3,4}
3. Persamaan eksponen dalam bentuk penjumlahan
Bentuk umum persamaan eksponen penjumlahan adalah sebagai berikut.
a. Bentuk eksponen harunya di uraikan samapai diperoleh bentuk yang sama. Untuk mrnguraikannya, gunakan sifat-sifat berikut
c. Selesaikan persamaanya, lalu subsitsikan kembali nilai variabel yang diperoleh pada permisalan.
untuk lebih jelasnya, simak contoh soal beerikut
contoh soal 3
tentukan solusi dari persamaan eksponen
pembahasan
misalnya 2^x = y, sehingga diperoleh:
Pertidaksamaan Eksponen
Pertidaksamaan Eksponen adalah pertidaksamaan jenis eksponen ysng memiliki variabel. Ternyata, pertidaksamaan eksponen memiliki dua bentuk umum yaitu sebagai berikut
untuk menentukan solusi pertidaksamaan di atas, ikuti langkah berikut.
1. bentuk eksponen harus diuraikan sampai diperoleh bentuk yang sama. uraikan berdasarkan sifat-sifat ekspinen.
2. Gunakan permisalan bentuk eksponen dengan variabel tertentu
3. Selesaikan pertidaksamaannya menggunakan konsep pertidaksamaan sampai diperoleh interval untuk permisalannya
4. Substitusikan nilai yang baik yang diperoleh pada permisalan.
Agar tambah paham dengan pertidaksamaan eksponen, perhatikan contoh berikut.
contoh soal 4
Tentukan himpunan penyelesaian dari pertidaksamaan eksponen
Pembahasan
untuk menentukan solusinya, harus menyamakan baris pada kedua ruas. Bertdasarkan eksponen diperoleh:
Selanjutnya, harus menempatkan titik pembuat nol dalam garis bilangan. Kemudian, tentukan tanda daerahnya dengan titik uji. Oleh karena tanda pertidaksamaannya "<", maka bulatannya kosong dan titik pembuat nol tidak termasuk dalam nilai x.
sekian yang dapat saya sampaikan dalam blog ini semoga bermanfaat bagi pemca iya
sekian terima kasih
Langganan:
Postingan (Atom)