Simpangan Rata Rata

Pengertaian Simpangan Rata Rata
   Simpangan rata rata merupakan termasuk kedalam ukuran penyebaran data seperti halnya Varian dan Standar Deviasi. kegunaannya adalah untuk mengetahui seberapa jauh nilai data yang telah menyimpang dari rata-rata yang sebenarnya.
Rumus Simpangan Rata-Rata
sekumpulan data kuantitatif yang tidak dikelompokkan serta dinyatakan oleh x1,x2,....xn. Dari data tersebut dapat ditentukan simpangan rata-rata (Sr)  dengan menggunakan sebuah rumus sebagai berikut:

contoh soal 1
Hitunglah simpangan rata-rata dari data kuatitatif tersebut
12,3,11,3,4,7,5,11
Pembahasan
Maka, simpangan rata-ratanya adalah 3,25

Untuk sekumpulan data yang dinyatakan oleh x1,x2,......,xn dan amsing-masing nilai data tersebut mempunyai frekuensi f1,f2,..., fn maka diperoleh nilai simpangan rata-rata menggunakan rumus:
contoh soal 2
Hitunglah simpangan rata-rata nilai ulangan Matematika siswa Kelas XI MAN 2 Merdeka seperti Tabel 1 dibawah berikut:
Tabel 1. Nilai ulanagan Matematika siswa kelas XI MAN 2 Merdeka

penyelesaian:
Dari tabel diatas, diperoleh = 65,7 (dibulatkan)

Maka, simpangan rata-rata  = 671,7/71= 9,46simpangan rataan hitung tersebjut menunjukkan rataan hitung jauhnya datum dari rataan hitung.
untuk menghitung simpangan baku dari data kuantitatif: 2,5,7,4,3,11,3 dengan kalkulator ilmiah (fx-3600Pv) ialah sebagai berikut:

Selanjutnya yaitu membahas simpangan rata-rata yang dibagi menjadi dua:
 1. Simpangan Rata-Rata dengan Data Tunggal
      Rumus Varian S^2 dari data tunggal
Rumus varian /ragam dari data tunggal ialah yang dinyatakan melalui persamaan dibawah berikut:

keterangan:

Rumus Standar Deviasi/Simpangan bakunya data tunggal ialah:
Rumus simpangan baku dan tunggal dinyatakan melalui sebuah persamaan dibawah ini

keterangan:

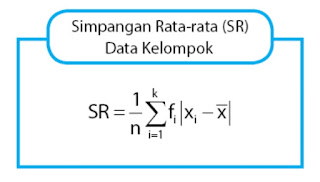
2. Simpangan Rata-Rata data berkelompok
runus:

keterangan:

Variasi (Ragam)
Persamaan untuk ragam atau variasi diberikan rumus sebagai berikut:

Standar Deviasi ( simpangan baku)
Rumus:

keterangan:

contoh soal dan pembahasannya
Diketahui sebuah data terurut (3x - 3), 2x,(2x + 1), (3x - 1), (3x + 3), dan (4x + 1). Jangkauan data tersebut ialah 6. Simpangan rata-rata dat tersebut yaitu.....

Pembahasannya:
Diketahui sebuah data berurut ialah sebagai berikut:
(3x -3), 2x (2x + 1), (3x -1), (3x +3), (4x + 1)
Nilai minimum =Xmin = 3x - 3
Nilai maksimum = X max + 4x + 1

jangkauan = Xmax- Xmin
6 = 4x +1 - (3x -3)
6 = 4x + 1 - 3x + 3
6 = x + 4
x = 2
Maka, daftar nilainya yaitu:
(3x - 3) = 3.2 -3 = 6 - 3= 3
2x = 2.2 = 4
2x + 1 = 2.2 + 1= 4 + 1= 5
3x - 1 = 3.2 -1 = 6 - 1 = 5
3x + 3 = 3.2 +3 = 6 + 3= 9
4x + 1 = 4.2 + 1 = 8 + 1 = 9
Maka, daftar nilainya yaitu:
(3x - 3) = 3.2 - 3 = 6 -3 = 3
2x = 2.2 = 4
2x + 1= 2.2 + 1 = 4 +1 = 5
3x -1 = 3.2 -1 = 6 - 1 = 5
3x + 3 = 3.3 + 3 = 6 + 3 = 9
4x + 1 = 4.2 + 1 = 8 + 1 = 9
oleh karena itu diperoleh data 3,4,5,5,7,9,9,

mencari rata-ratanya adalah:

mencari simpangan rata-ratanya ialah

 Mungkin cukup sampai disini yang dapat saya jelaskan pada artikel ini
semoga bermanfaat iya bagi pembaca semua.