Persamaan linier dapat dinyatakan sebagai matriks. Misalnya persamaan:
dapat dinyatakan dalam matriks ter agumentasikan sebagai berikut ini
Penyelesaian persamaan linier dalam bentuk matriks dapat dilakukan melalui beberapa cara yaitu eliminasi Gauss atau dapat juga dengan cara eliminassi Gauss- Jordan. Namun, suatu sistim persamaan linier dapat diselesaikan dengan eliminasi Gauss untuk mengubah bentuk matriks teraugumentasi ke dalam bentuk eselon-baris tanpa menyederhanakan nya. cara ini disebut dengan subsitusi balik.
Penyelesaian Persamaan Linier dengan Matriks (Bagian 1)
Bentuk eselon-baris (M=Rumus Ideal)
- di setiap baris, angka pertama selain 0 harus 1 (leading 1)
- jika ada baris yang semua elemennya 0, maka harus dikelompokkan dibaris akhir dari matriks.
- jika ada baris yang leading 1 maka leading 1 di bawahnya , angka 1-nya harus berada lebih kanan dari leading 1 diatasnya
- jika kolom yang memiliki leading 1 angka selain 1 adalah nol maka matriks tersebut disebut Eleson-baris tereduksi
- syarat 1: baris pertama disebut dengan leading 1
- syarat 2: baris ke-3 dan ke-4 memenuhi syarat 2
- syarat 3: baris pertama dan ke-2 memenuhi syarat 3
- syarat 4 : matriks dibawah ini memenuhi syarat ke-4 dan disebut Eselon-bars tereduksi
Eliminasi Gaus adalaah suatu cara mengoperasikam nilai-nilai dalam matriks sehingga menjadi matriks lebih sederhana (ditemukan oleh carl priedrich Gauss). Cranya adalah dengan malakukan operasi baris sehingga matriks tersebut menjadi matriks yang Eselon-baris. Ini dapat digunakan sebagai salah satu metode penyelesaian persamaan linier dengan menggunakan matriks. caranya dengan mengubah persamaan linier tersebut kedalam matriks teraugumentasi dan mengoperasikannya.
contoh:
Dikethui persamaan linier
tentukan nilai x,y dan z
jawab:
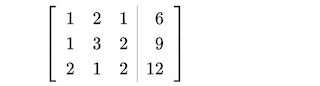
Bentuk persamaan tersebut kedalam Matriks
maka mendapatkan 3 persamaan linier baru yaitu:
kemudian lakukan subsitusi balik maka didapatkan:
jadi nilai x=3, y=0, dan z=3
Operasi Eliminasi Gauss-Jordan
Eliminasi Gauss-Jordan adalah pengembangan dari eliminasi gauss yang hasilnya lebih sederhana. caranya adalah dengan meneruskan operasi baris dari eliminasi Gauss sehingga menghasilkan matriks yang Eleson-baris tereduksi. ini juga dapat digunakan sebagai salah satu metode penyelesaian persamaan linier dengan menggunakan matriks. cara dengan mengubah persamaan linier tersebut kedalam matriks teraugementasi dan mengoperasikannya. setelah menjadi matriks Eleson-baris tereduksi, maka langsung dapat ditentukan nilai dari variabel-variabelnya tanpa subsitusi balik.
contoh:
diketahui persamaah linier
tentukan nilai x,y dan z
jawab:
Bentuk persamaan tersebut kedalam matriks
operasikan matriks tersebut
maka didapatkan nilai dari x = 2, y = -1, dan z = 1
munkin sampai disini saja yang dapat saya sampaikan dalam artikel ini semoga bermanfaat bagi pembaca






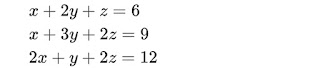


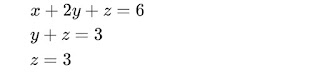










Tidak ada komentar:
Posting Komentar