Eksponen adalah bentuk perkalian suatu bilangan yang sama secara berulang-ulang. mungkin Quipperian biasa mendengar istilahnya sebagai bilangan berpangkat. contohnya sebagai berikut.
Bentuk eksponen bisa dinyatakan dalam bentuk persamaan maupun pertidaksamaan. Hal itu berkaitan dengan jenis penggunaanya, misalnya untuk menyelasaikan masalah yang berkaitan dengan fungsi eksponen.Nah, konsep dasar perkalian berulang-ulang inilah yang nantinya digunakan pemerintah untuk menghitung jumlah penduduk beberapa tahun ke depan. Tentunya dengan perhitungan dan penurunan rumus yang tidak mudah ya!
Persamaan Eksponen
1. Persamaan eksponen berbasis konstanta
untuk persamaan eksponen berbasis konstanta, terdapat dua persamaan yang harus dipahami,yaitu sebagai berikut.
untuk lebih jelasnya, simak contoh soal berikut ini,
contoh soal 1
pembahasan
untuk menentukan solusinya, harus menyamakan baris kedua ruas terlebih dahulu. Berdasarkan sifat-sifat eksponen, diperoleh:
2. Persamaan eksponen berbasis fungsi
Bentuk umum persamaan eksponen di atas memiliki empat kemungkinan solusi, yaitu sebagai berikut.
a. g(x) = h(x)
b. f(x) = 1
c. f(x) = -1, dengan syarat g(x) dan h(x) sama-sama genap atau ganjil
d. f(x) = 0, dengan syarat g(x),h(x) >0
contoh soal 2
pembahasan
solusi dari oersamaan eksponen diatas, didapat dari 4 kondisi berikut.
- solusi ke-1
- solusi ke-2
- solusi ke-3
uji pangakat untuk rusa kiri
uji pangkat untuk ruas kanan
x + 4 = 1 + 4 = 5 ( ganjil)
oleh karena sama-sama ganjil, maka x =1 merupakan penyelesaian
- solusi ke-4
uji pangkat ruas kiri
oleh karena 0 bukan bilangan positif, maka x = 2 bukan termasuk penyelesaian.
jadi, himpunan penyelesaian dari persamaan eksponen dia tas adalah {-1,1,3,4}
3. Persamaan eksponen dalam bentuk penjumlahan
Bentuk umum persamaan eksponen penjumlahan adalah sebagai berikut.
Lalu bagaimana langkah-langkah menentukan hasil persamaan eksponen dalam bentuk penjumlahan ini?
a. Bentuk eksponen harunya di uraikan samapai diperoleh bentuk yang sama. Untuk mrnguraikannya, gunakan sifat-sifat berikut
b. gunakan permisalannya bentuk eksponen yang sama dengan variabel tertentu.
c. Selesaikan persamaanya, lalu subsitsikan kembali nilai variabel yang diperoleh pada permisalan.
untuk lebih jelasnya, simak contoh soal beerikut
contoh soal 3
tentukan solusi dari persamaan eksponen
pembahasan
misalnya 2^x = y, sehingga diperoleh:
Subsitusikan nilai balik y pada permisalan tersebut.
Jadi, solusi dari persamaan di atas adalah x = 3
Pertidaksamaan Eksponen
Pertidaksamaan Eksponen adalah pertidaksamaan jenis eksponen ysng memiliki variabel. Ternyata, pertidaksamaan eksponen memiliki dua bentuk umum yaitu sebagai berikut
:
untuk menentukan solusi pertidaksamaan di atas, ikuti langkah berikut.
1. bentuk eksponen harus diuraikan sampai diperoleh bentuk yang sama. uraikan berdasarkan sifat-sifat ekspinen.
2. Gunakan permisalan bentuk eksponen dengan variabel tertentu
3. Selesaikan pertidaksamaannya menggunakan konsep pertidaksamaan sampai diperoleh interval untuk permisalannya
4. Substitusikan nilai yang baik yang diperoleh pada permisalan.
Agar tambah paham dengan pertidaksamaan eksponen, perhatikan contoh berikut.
contoh soal 4
Tentukan himpunan penyelesaian dari pertidaksamaan eksponen
Pembahasan
untuk menentukan solusinya, harus menyamakan baris pada kedua ruas. Bertdasarkan eksponen diperoleh:
oleh karena a =7>1, maka berlaku:
Titik pembuat nol x = 4 dan x = 2
Selanjutnya, harus menempatkan titik pembuat nol dalam garis bilangan. Kemudian, tentukan tanda daerahnya dengan titik uji. Oleh karena tanda pertidaksamaannya "<", maka bulatannya kosong dan titik pembuat nol tidak termasuk dalam nilai x.
Jadi, Himpunan penyelesaian dari pertidaksamaan eksponen di atas adalah {x| x E R, 2 < x < 4}
sekian yang dapat saya sampaikan dalam blog ini semoga bermanfaat bagi pemca iya
sekian terima kasih





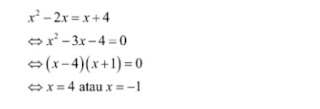











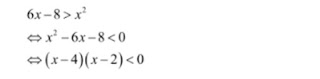

Tidak ada komentar:
Posting Komentar