Menyelesaikan Sistem Persamaan Linier Dua Varibel Dengan Metode Grafik

       Menyelesaikan Persamaan Linier Dua Variabel Dengan Metode Grafik

Pada metode grafik, himpunan penyelesaian dari sisitem persamaan linier dua variabel adalah koordinat titik potong dua garis tersebut. Jdi Anda harus mencari titik potong garis tersebut di koordinat y dengan membuat x = 0 yang akan berpotongan di (0,y), dan mencari titik potong garis tersebut dikoordinat x dengan membuat y =0 yang akan berpotongan di (x,0). Kemudian menarik kedua garis tersebut sehingga berpotongan di suatu titik koordinat (x,y). Untuk menetapkan pemahaman Anda silahkan simak contoh berikut ini:

contoh;
Dengan metode grafik, tentukan himpunan penyelesaian sistem persamaan linier dua variabel x+y = 4 dan x+3y = 6 jika x,y variabel pada himpunan bilangan real.

penyelesaian:
seperti telah dijelaskan di atas, Anda harus mencari koordinat titik potong di x dan y pada persamaan x + y =4 dan x + 3y = 6. Sekarang kita cari titik potong di x dan y persamaan x + y = 4, yakni:
jika x =0 maka,
x + y = 4
0 + y = 4
y = 4 => titik potong di y (0,4)

jika y = 0 maka,
x + y = 4
x + 0 =4
x = 4 => titik potong di x (4,0)
jadi titik potong persamaan x +y =4 adalah (0,4) dan (4,0)

kita cari titik potong di x dan y persamaan x + 3y = 6 yakni,
jika x = 0, maka:
x + 3y = 6
0 +3y = 6
     3y = 6
       y = 6/3
       y = 2  => titik potong di y (0,2)

jika y = 0, maka:
x + 3y    = 6
x + 3(0) = 6
x +0      = 6
          x = 6   => titik potong di x (6,0)
jadi titik potong dari persamaan x = 3y = 6 adalah (0,2) dan (6,0)
Sekarang baut garis dari dua persamaan tersebut berdasarkan titik potong, yakni seperti gambar dibawah ini

Berdasarkan gambar grafik persamaan dari x + y = 4 dan x + 3y = 6 di atas tampak bahwa koordinattitik potong krdua garis adalah (3,1)

Jadi, himpunan penyelesaian dari sistem persaman x + y = 4 dan x + 3y = 6 adalah (3,1)


contoh 2
 Dengan metode grafik, tentukan himpunan penyelesaian sisitem persamaan linier dua variabel x + 2y = 2 dan 2x + 4y = 8 jika x,y variabel pada himpunan bilangan real.

Penyelesaian :
sekarang kita cari titik potong x dan y dari persamaan x + 2y =2
jik x =0, maka:
x + 2y = 2
0 + 2y = 2
        y = 1  => titik potong di y (0,1)

jika y = 0, maka :
x + 2y = 2
x+ 2(0) = 2
x + 0 = 2
x = 2  => titik potong di x (2,0)

jadi titik potong persamaan x + 2y = 2 adalah (0,1) dan (2,0)

kita cari titik potong x dan y pada persamaa 2x +4y = 8
jika x = 0 maka:
2x + 4y = 8
2(0) + 4y = 8
    0  + 4y = 8
             y = 2   => titik potong di y (0,2)

jika y = 0, maka:
2x + 4y = 8
2x + 4(0) = 8
2x + 0 = 8
        x = 4     => titik potong di x (4,0)
jadi titik potong persamaan 2x + 4y + 8 adalah (0,2) dan (4,0)

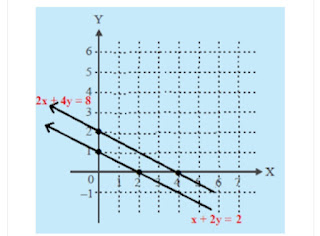
sekarang buat garis dari kedua persamaan tersebut berdasarkan titik potong, yakni seperti gambar berikut ini.

Berdasarkan garfik sistem persamaan dari x + 2y = 2 dan 2x + 4y = 8 diatas nampak bahwa keduanya tersebut tidak akan pernah berpotongan. Jadi, himpunan penyelesaian dari sistem persamaan  x+ 2y = 2 dan 2x + 4y = 8 adalah himpunan {}




selamat membaca dan semoga bermanfaat.......